Fundamentals of Linear Algebra: Vectors, Matrices, and Scalars
Linear algebra is a foundational branch of mathematics that focuses on vectors, matrices, scalars, and their interrelations. These elements are crucial in various fields, including physics, engineering, and computer science. This article delves into these fundamental concepts and their operations.
Vectors
A vector is a quantity that has both magnitude and direction. In a two-dimensional space, a vector is often represented as an arrow pointing from the origin (0, 0) to a specific point (x, y). Vectors can also exist in higher-dimensional spaces. Each component of a vector represents a magnitude along a specific dimension. Vectors are often denoted by bold letters (e.g., v) or by listing their components, such as v = [x, y].
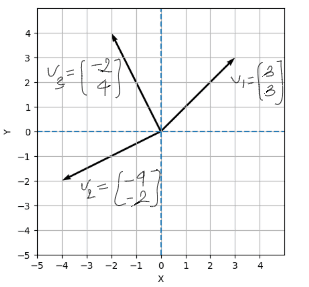
The image shows a 2D coordinate system with three vectors represented as arrows starting from the origin [0,0]. Each vector is also labeled with its component form:
This vector points up and to the right.
It extends 3 units along the x-axis and 3 units along the y-axis.
Because both components are equal, the vector lies along the line y = x, forming a 45° angle with the x-axis.
This indicates both horizontal and vertical movement are equal in magnitude.
This vector points down and to the left.
It moves 4 units in the negative x-direction and 2 units in the negative y-direction.
Its direction is angled more horizontally than vertically.
It lies in the third quadrant, where both x and y components are negative.
This vector points up and to the left.
It moves 2 units in the negative x-direction and 4 units in the positive y-direction.
It lies in the second quadrant.
The vertical component is greater than the horizontal one, so the vector is more "vertical" in its direction.
These samples demonstrate how vectors can be visualized and compared in direction, length (magnitude), and component form.
Scalars
Scalars are single numerical values that serve to scale vectors and matrices during mathematical operations. They are constants that, when multiplied with vectors or matrices, change their magnitude without affecting their structural integrity.
In fact, scalars are nothing new—they are simply the real numbers you already use in everyday life. From now on, we refer to them as scalars when they are used in the context of vectors and matrices, to highlight the fact that they can scale vectors but do not have any direction themselves.
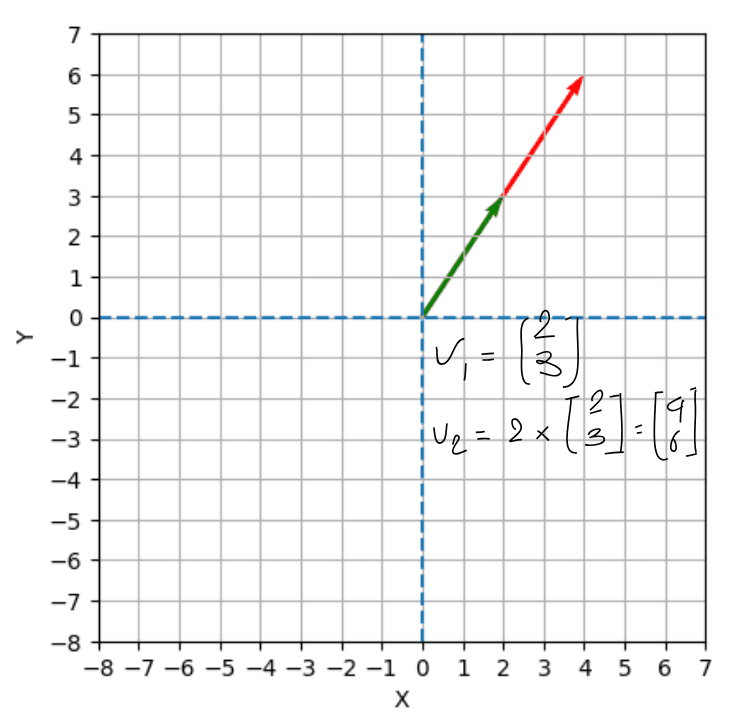
This image illustrates how a scalar multiplies a vector to produce a new vector that has the same direction but a different magnitude. The original vector is shown in green, starting from the origin and pointing to the coordinates (2, 3). When this vector is multiplied by the scalar 2, it becomes , shown in red. As you can see, the new vector has the same direction as the original vector, but it is twice as long. This demonstrates that scalars can stretch or shrink vectors, affecting their magnitude while preserving their direction.
Scalars generally cannot change the direction of vectors; they only affect the magnitude. However, there is one exception—when the scalar is less than zero, it reverses the vector, pointing it in the exact opposite direction. For example, take the vector v=[2,3] and multiply it by -1. The result is:
This new vector keeps the same length but points in the opposite direction. So, while scalars cannot give a vector a new direction in space, they can flip it completely if the scalar is negative.
Matrices
A matrix is a rectangular array of numbers arranged in rows and columns. The dimensions of a matrix are specified by the count of its rows and columns. For instance, an "m x n" matrix comprises m rows and n columns. Matrices are denoted by uppercase letters (e.g., A, B), and their individual elements are often referenced using subscripts, such as indicating the element in the ith row and jth column.
In linear algebra, each row and each column of a matrix can be interpreted as vectors. These vectors are instrumental in representing and manipulating data across various mathematical and computational applications. For example, consider a 2x3 matrix:
Here, the rows [1 2 3] and [4 5 6] can be viewed as vectors in a three-dimensional space, while the columns [1 4], [2 5], and [3 6] can be regarded as vectors in a two-dimensional space.
Square Matrices and Identity Matrices
A square matrix is one where the number of rows equals the number of columns, forming an n × n matrix. A notable example of a square matrix is the identity matrix, denoted as I. The identity matrix is characterized by ones on its main diagonal (from the top left to the bottom right) and zeros elsewhere. It serves as the multiplicative identity in matrix operations, meaning that any matrix multiplied by the identity matrix remains unchanged. Wikipedia
Vector and Matrix Operations
Linear algebra encompasses a variety of operations involving vectors and matrices:
Addition and Subtraction: These operations involve adding or subtracting corresponding elements of two matrices of identical dimensions to produce a new matrix of the same size. For example, if A and B are two matrices of the same dimensions, their sum A + B results in a matrix C where each element C[i][j] is the sum of A[i][j] and B[i][j].
Scalar Multiplication of Vectors: This operation entails multiplying each component of a vector by a scalar, thereby altering the vector's magnitude without changing its direction. For instance, if v = [x, y], then multiplying by 2 yields 2v = [2x, 2y].
Transpose: Transposing a matrix involves swapping its rows with its columns. If A is an m x n matrix, its transpose, denoted as A^T, becomes an n x m matrix where the rows of A become the columns of A^T and vice versa. Transposition is a fundamental operation utilized in various matrix computations and transformations.
Understanding these core concepts and operations of linear algebra is essential for delving into more advanced topics and applications within mathematics and related disciplines.